In the field of mathematics, discrete graph theory has emerged as a significant area of study that deals with discrete structures and their relationships. The theory is focused on graphs, which are mathematical tools used to represent a set of objects and the connections between them. In this post, we will explore some of the basics of discrete graph theory and its applications.
What is a graph?
A graph is a mathematical construct composed of a set of objects, called vertices, and a set of connections between them, called edges. A graph is typically represented visually as a set of points connected by lines or curves. Graphs can be directed or undirected, and weighted or unweighted, depending on the nature of the connections between the vertices.
Applications
Discrete graph theory has a wide range of applications in various fields including computer science, engineering, physics, and social sciences. One of the most widely used applications of graph theory is in computer networking. Graph theory is used to model the connections between devices in a network, which can help to optimize network performance and troubleshoot connectivity issues.
Another application of graph theory is in social network analysis. Social networks can be represented as graphs, with the vertices representing individuals or entities and the edges representing connections or relationships between them. By analyzing these graphs, researchers can gain insights into the structure and dynamics of social networks, and identify key players or groups.
Graph theory is also used in operations research and logistics, where it is used to solve problems related to transportation, scheduling, and resource allocation. Graph algorithms are used to optimize routes, minimize costs, and maximize efficiency in a wide range of applications.
Conclusion
Discrete graph theory is a fascinating area of study that has a wide range of practical applications. From computer networking to social network analysis to operations research, graph theory provides a powerful set of tools for modeling and understanding complex systems. Whether you are a mathematician, computer scientist, engineer, or social scientist, graph theory is a field that is sure to provide new insights and opportunities for research and innovation.
If you are looking for Mathematics | Graph Theory Basics - Set 1 - GeeksforGeeks you've visit to the right web. We have 6 Pictures about Mathematics | Graph Theory Basics - Set 1 - GeeksforGeeks like Mathematics | Graph Theory Basics - Set 1 - GeeksforGeeks, discrete mathematics - How to justify the statement that a graph is and also discrete mathematics graph theory. Here you go:
Mathematics | Graph Theory Basics - Set 1 - GeeksforGeeks
www.geeksforgeeks.org (PDF) Discrete Mathematics And Graph Theory. 2nd Ed
www.researchgate.net theory mathematics discrete graph 2nd ed pdf
Nota Math Discrete Graph Theory
www.slideshare.net Discrete Mathematics Lecture 18: Graph Theory Basics - YouTube
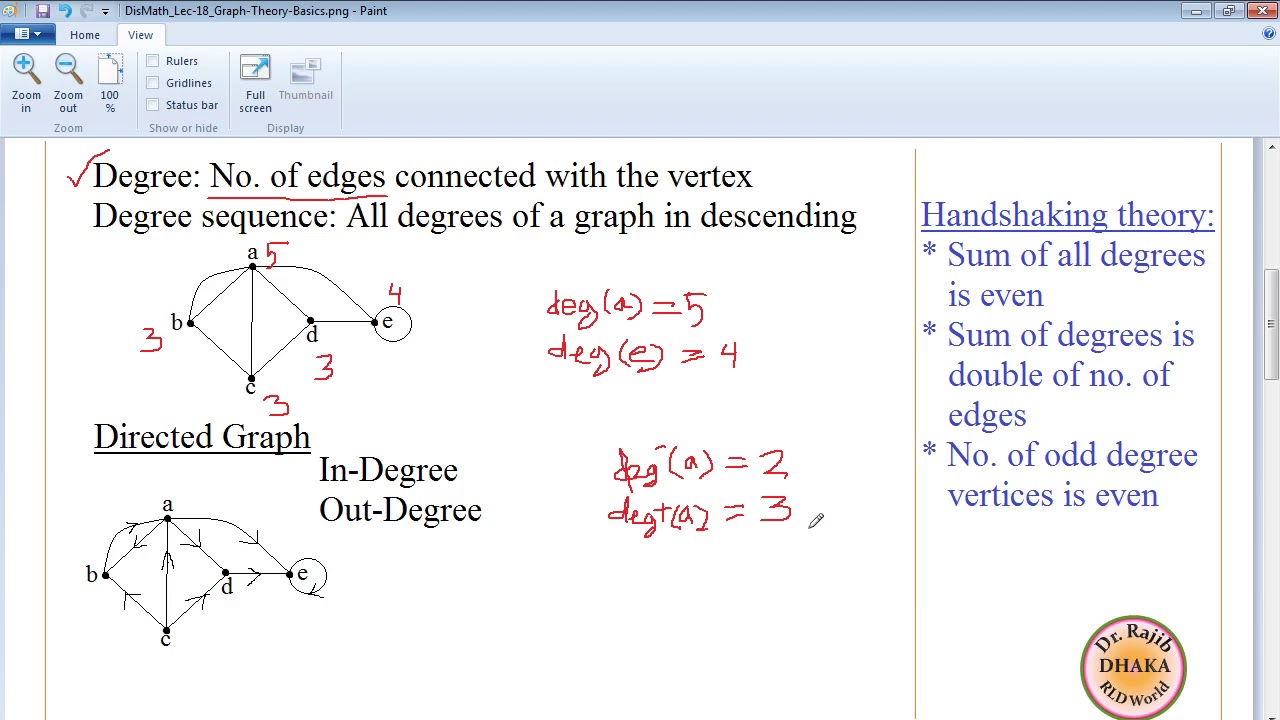www.youtube.com discrete mathematics theory
Discrete Mathematics Graph Theory
boniyeamincse.blogspot.com discrete vertex
Discrete Mathematics - How To Justify The Statement That A Graph Is
math.stackexchange.com graph discrete mathematics connected justify statement math theory connectedness stack
Discrete mathematics. Graph discrete mathematics connected justify statement math theory connectedness stack. Discrete mathematics lecture 18: graph theory basics
0 Post a Comment: