What's up, beautiful people! Today we're talking about something a little different, but still just as important as anything else in life. We're talking about discrete mathematics and functions. Now, before you tune out, let me just say that this is actually pretty interesting stuff. And don't worry about whether or not you're "smart enough" to understand it, because I'm going to break it down for you so even your grandma can understand.
Functionality is key
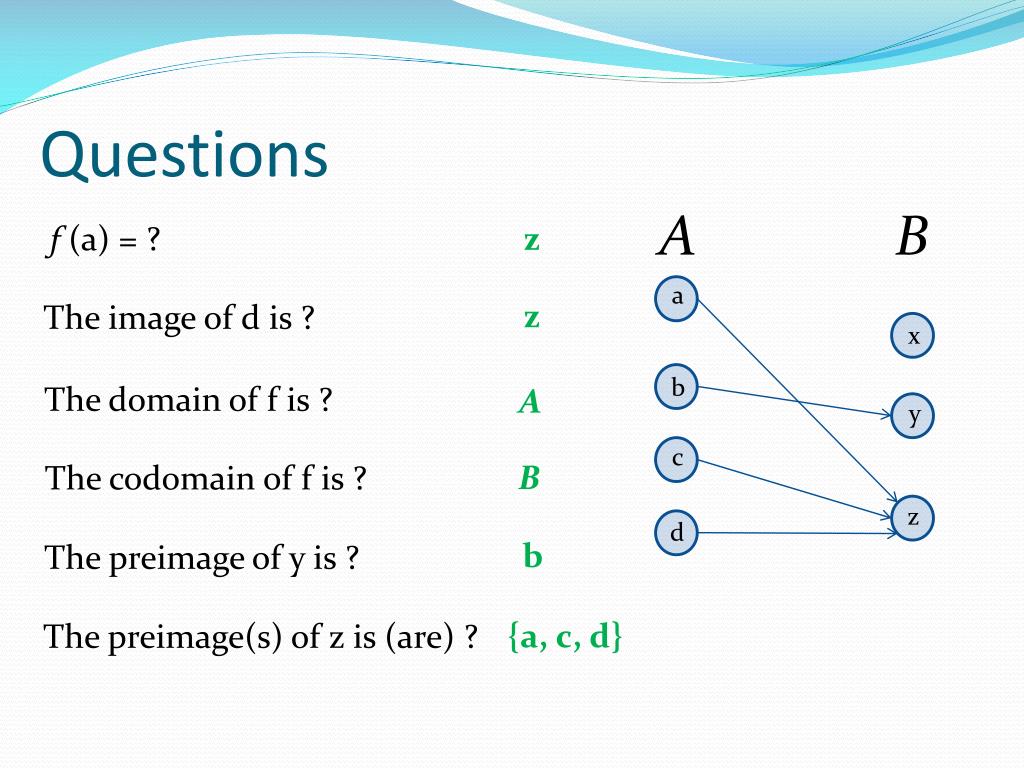
So let's start with what a function actually is. In math terms, a function is just a relationship between two sets. It's a way of taking one set (let's call it X) and associating each element of that set with a unique element from another set (let's call it Y). The key here is that each element in X can only be associated with one element in Y, and every element in Y has to be associated with at least one element in X.
Now I know, that all sounds incredibly boring, but stick with me here. Functions are actually super important in a lot of different fields, including computer science, economics, and even engineering. Without functions, we wouldn't be able to write algorithms, model complex systems, or even calculate basic statistics. So even if you're not a math nerd like me, you can still appreciate the power of functions.
Congruent or Nah?
But wait, there's more! Let's talk about congruence. In math terms, congruence basically means "the same as". So if I say that 1 is congruent to 4 modulo 3, that just means that when you divide 1 and 4 by 3, you get the same remainder (which is 1). Makes sense, right?
But here's where things get a little tricky. You might see something called "equivalence classes" when you're studying congruence, and that's where the notation [a] comes in. Basically, [a] just means "the set of all numbers that are congruent to a". So if we take our example from before, [1] would be the set 1, 4, 7, 10, ... (since all of those numbers leave a remainder of 1 when divided by 3).
The Final Word
So there you have it, folks. A (somewhat) quick and dirty overview of discrete mathematics and functions. I hope I didn't scare you off too much, and maybe even convinced you that math isn't so bad after all. And if you're still not convinced, well, at least you know a little bit more about what those math nerds are talking about.
If you are searching about discrete mathematics - Is $[a]_R$ the same as [a]? - Mathematics Stack you've came to the right page. We have 6 Images about discrete mathematics - Is $[a]_R$ the same as [a]? - Mathematics Stack like Discrete Math 1 - Tutorial 50 - Sets and Subsets, "Not" Subsets - YouTube, discrete mathematics - Is $[a]_R$ the same as [a]? - Mathematics Stack and also Discrete Math 1 - Tutorial 50 - Sets and Subsets, "Not" Subsets - YouTube. Here it is:
Discrete Mathematics - Is $[a]_R$ The Same As [a]? - Mathematics Stack
math.stackexchange.com discrete mathematics math stack same susanna epp applications source
Discrete Math 1 - Tutorial 50 - Sets And Subsets, "Not" Subsets - YouTube
www.youtube.com discrete math sets tutorial subsets
Discrete Mathematics Sets - презентация онлайн
ppt-online.org discrete mathematics sets ppt
Discrete - DriverLayer Search Engine
driverlayer.com discrete descrete
PPT - Discrete Mathematics: Functions PowerPoint Presentation, Free
www.slideserve.com discrete functions mathematics sets question domain ppt powerpoint presentation questions
Discrete Math: Intro To Relations - YouTube
www.youtube.com discrete math relations intro
Discrete mathematics sets. Discrete math relations intro. Discrete math sets tutorial subsets
0 Post a Comment: